Introducción
La transformada de Laplace
es una herramienta de gran alcance formulada para solucionar una variedad
amplia de problemas de inicial valor. La estrategia es transformar las
ecuaciones diferenciales difíciles en los problemas simples de la algebra donde
las soluciones pueden der obtenidas fácilmente. Entonces se aplica la
transformada inversa de Laplace para recuperar las soluciones de los problemas
originales.
Es un procedimiento
desarrollado por el matemático y astrónomo francés Pierre Simón Marques de
Laplace (1749-1827) que permite cambiar las funciones de la variable del tiempo
t a una función de la variable compleja s.
Las características
fundamentales de la transformada Laplace son:
- Es un método operacional que pueden usarse para resolver ecuaciones diferenciales lineales.
- Las funciones senoidales, senoidales amortiguadas y exponenciales se pueden convertir en funciones algebraicas lineales en la variable s.
- Sirve para reemplazar operaciones como derivación e integración, por operaciones algebraicas en el plano complejo de la variable s.
- Este método permite usar técnicas gráficas para predecir el funcionamiento de un sistema sin necesidad de resolver el sistema de ecuaciones diferenciales correspondiente.
Transformada de Laplace
Es un método operacional que puede usarse
para resolver ecuaciones diferenciales lineales. Con el uso de la transformada
de Laplace muchas funciones sinusoidales y exponenciales, se pueden convertir
en funciones algebraicas de una variable s, y reemplazar operaciones como la
diferenciación y la integración, por operaciones algebraicas en el plano
complejo.
Por qué Transformada de Laplace?
En el estudio de los
procesos es necesario considerar modelos dinámicos, es decir, modelos
de comportamiento variable respecto al tiempo. Esto trae como consecuencia
el uso de ecuaciones diferenciales respecto al tiempo para
representar matemáticamente el comportamiento de un proceso.
El comportamiento dinámico
de los procesos en la naturaleza puede representarse de
manera aproximada por el modelo general de
comportamiento dinámico lineal.
La transformada de Laplace
es una herramienta matemática muy útil para el análisis
de sistemas dinámicos lineales.
De hecho, la transformada de
Laplace permite resolver ecuaciones diferenciales lineales
mediante la transformación en ecuaciones algebraicas con lo cual se facilita su
estudio.
Una vez que se ha estudiado
el comportamiento de los sistemas dinámicos, se puede proceder a diseñar y
analizar los sistemas de control de manera simple.
Para qué sirve la transformada de
Laplace?
Puede ser usada sencillamente para resolver ecuaciones
diferenciales, lineales e integrales.
- En la instrumentación y control: el campo de la aplicación de los sistemas de control es muy amplio y esta transformada a menudo se emplea en los análisis dinámicos de instrumentos ya que es una herramienta fácil para resolver sistemas de procesos donde se deben emplear diagramas de bloques, para así representar cada componente físico de la señal.
- En el estudio de procesamiento de señales digitales, como son el análisis de circuitos digitales, los sistemas de radar o telecomunicaciones y especialmente los sistemas de control de procesos por computadoras.
- En instrumentación, la ventaja de trabajar con las transformaciones de Laplace es que existen tablas de conversión muy extensas que cubren prácticamente la totalidad de sus funciones que puedan surgir al analizar los sistemas controlados.
Cálculos de la
transformada de Laplace
La transformada de
Laplace es un tipo de transformada
integral frecuentemente
usada para la resolución de ecuaciones
diferenciales ordinarias. La transformada de Laplace de una función ¦(t) definida para todos los números positivos t ≥ 0, es la función.
Propiedades de las transformadas de
Laplace
1. Linealidad
La transformada de Laplace se distribuye sobre las sumas o restas y saca constantes que multiplican.
Versión para la inversa:
2. Primer teorema de
traslación
Donde
La
transformada de Laplace se convierte un factor exponencial en una traslación en
la variable s.
Versión
para la inversa:
3. Teorema de la
transformada de la derivada
La
transformada de Laplace cancela la derivada multiplicando por la variable s.
4. Teorema de la
transformada de la integral
5. Teorema de la
integral de la transformada
Siempre
y cuando exista
6. Transformada de la
función escalón o función de Heaviside
u(t-a) o H(t-a)
Representa
la función de escalón unitario
La
transformada de Laplace u(t-a)
7. Segundo
teorema de traslación
8. Transformada de
una función periódica
Si
f(t) es una función periódica con período T:
9. Teorema de la
convolución
La convolución es una cuenta que se realiza con dos
funciones que da como resultado una nueva función
Si f * g representa la convolución entre las
funciones f y g entonces
Tabla de transformada de Laplace
1. Con la ayuda de la tabla hallemos la
transformada de Laplace de la función.
f(x)
= 3 + 2 x²
Utilizando la propiedad 1, de linealidad de las transformadas, y con
ayuda de la tabla tenemos:
2. Con la ayuda de la tabla hallemos F(s) para la función f(x)
= 2 sen x + 3 cos 2x.
Utilizando la linealidad,
y mediante la tabla tenemos:
3. Con la ayuda de la tabla hallar F(s) para la función f(x)
= x e4x .
y la propiedad de las transformadas, tenemos:
4. Con la ayuda de la tabla hallar F(s) para la función f(x)
= x cos 7x .
Respuesta: Según la tabla, la transformada para f(x) = x cos 7x
es:
Entonces, teniendo en cuenta la propiedad de las
transformadas, tenemos:
L(x cos 7x)= s^2-49/(s^2+49)^2
Ejercicio demostrativo aplicado a la Instrumentación y
control
Para un proceso de un tanque
con un área transversal de 50 m2 y un flujo de salida de (h)/4, dibuje el
diagrama de proceso determine el modelo de la ecuación diferencial y luego
obtenga a partir de la ecuación diferencial el modelo de función de
transferencia mediante la transformada de la Laplace.
FUENTE DE INFORMACION







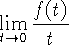




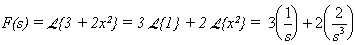





No hay comentarios:
Publicar un comentario